SKKN Phân loại và phương pháp giải các bài tập giao thoa ánh sáng có nhiều thành phần đơn sắc
Bạn đang xem tài liệu “SKKN Phân loại và phương pháp giải các bài tập giao thoa ánh sáng có nhiều thành phần đơn sắc”, để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
1. MỞ ĐẦU - LÝ DO CHỌN ĐỀ TÀI Trong thời kỳ phát triển của đất nước hiện nay, đặt ra cho nghành giáo dục phải đổi mới, nâng cao chất lượng giảng dạy nhằm đào tạo nguồn nhân lực chất lượng cao, tiếp cận được với khoa học công nghệ hiện đại. Vật Lý học là một bộ môn khoa học cơ bản đóng vai tṛò nền tảng, cung cấp cơ sở lý thuyết cho một số môn khoa học ứng dụng. Sự phát triển của Vật lý học có vai tṛò quan trọng dẫn tới sự xuất hiện nhiều ngành kỹ thuật mới như: Kỹ thuật điện tử, Kỹ thuật tự động hoá, Công nghệ tin học Mục tiêu giảng dạy Vật lý ở trường Trung học phổ thông nhằm cung cấp cho học sinh những kiến thức cơ bản về Vật lý và những ứng dụng của Vật lý trong sản xuất và đời sống. Giúp các em lĩnh hội kiến thức có hiệu quả và tạo cho các em sự hứng thú học tập môn Vật lý, lòng yêu thích, tính trung thực trong khoa học và sẵn sàng áp dụng những kiến thức Vật lý đã học vào thực tế cuộc sống hàng ngày. Biết vận dụng những kiến thức đã học vào việc giải bài tập Vật lý là một trong những phương pháp để khắc sâu kiến thức cho học sinh. Với mỗi vấn đề, mỗi dạng bài tập, người giáo viên cần gợi ý, hướng dẫn để các em có thể chủ động tìm ra cách giải nhanh nhất, hiệu quả nhất khi làm bài tập. Trong quá trình giảng dạy, tôi nhận thấy khi giải bài tập tập về: “Giao thoa ánh sáng có nhiều thành phần đơn sắc”, của chương trình Vật lý lớp 12 là loại bài tập khó, trìu tượng, các em học sinh thường bị lúng túng trong việc tìm cách giải, hơn nữa trong bài toán này các em thường xuyên phải tính toán dài, dể bị nhầm lẫn, dẫn đến kết quả không chính xác. Bộ giáo dục và Đào tạo trong những năm gần đây liên tục đổi mới cách kiểm tra đánh giá học sinh để phù hợp với yêu cầu xã hội, đòi hỏi học sinh phải có tư duy mạch lạc, kỷ năng giải toán nhanh và chính xác, mới đáp ứng được yêu cầu đã đặt ra. Qua đọc một số tài liệu tham khảo, các đề tài sáng kiến kinh nghiệm của bạn bè, đồng nghiệp viết về giao thoa ánh sáng nhưng chưa có tài liệu, đề tài nào chuyên sâu để giải các bài toán về “giao thoa ánh sáng có nhiều thành phần đơn sắc ”. Xuất phát từ thực tế đó, với một số kinh nghiệm bản thân trong quá trình giảng dạy để giải quyết vấn đề khó khăn, vướng mắc nói trên tôi chọn đề tài “ Phân loại và phương pháp giải các bài tập giao thoa ánh sáng có nhiều thành phần đơn sắc” để nghiên cứu. Qua đây giúp các em học sinh có thể hiểu bài nhanh chóng, nắm được cách giải chính xác và chủ động hơn khi gặp những bài toán dạng này, tạo được hứng thú cho học sinh học tập môn Vật lý. - MỤC ĐÍCH NGHIÊN CỨU Giúp học sinh hiểu rõ hiện tượng giao thoa ánh sáng, nắm vững các dạng bài tập về hiện tượng giao thoa ánh sáng gồm hai hoặc ba thành phần đơn sắc và biết vận dụng linh hoạt để giải các bài toán dạng này khi gặp phải trong các kỳ thi, đặc biệt là kỳ thi THPT Quốc gia. Rèn luyện kỹ năng vận dụng kiến thức toán học và sử dụng máy tính cầm tay vào việc giải nhanh các bài toán Vật lý. Giáo dục kỹ thuật tổng hợp: học sinh giải thích được một cách định tính và định lượng về hiện tượng giao thoa ánh sáng thường gặp trong đời sống. - ĐỐI TƯỢNG NGHIÊN CỨU + Các dạng bài tập về giao thoa ánh sáng có nhiều thành phần đơn sắc” thuộc: Chương V- Sóng ánh sáng - Chương trình Vật lý lớp 12 THPT. + Học sinh lớp 12 trường THPT Đông Sơn 1 - PHƯƠNG PHÁP NGHIÊN CỨU + Phương pháp điều tra khảo sát thực tế, thu thập thông tin. + Phương pháp thống kê, xử lý số liệu. + Phương pháp thực nghiệm. 2. NỘI DUNG 2.1. Cơ sở lý luận. Trong chương trình sách giáo khoa Vật lý 12 cơ bản học sinh được học về giao thoa sóng ánh sáng, thì nguồn sáng chỉ là ánh sáng đơn sắc, nhưng khi làm bài tập học sinh lại gặp phải những bài toán nguồn sáng gồm nhiều thành phần đơn sắc, khi đó các dạng vừa đa dạng, vừa phức tạp. Các tài liệu tham khảo đang dược lưu hành hiện nay đã đề cập đến các bài tập về giao thoa đối với nguồn đơn sắc, nguồn sáng trắng nhưng ở mức độ đơn giản, còn các dạng bài tập của nguồn sáng gồm nhiều thành phần đơn sắc thì chưa được đề cập đến một cách đầy đủ và sâu rộng. 2.2. Thực trạng vấn đề trước khi áp dụng sáng kiến kinh nghiệm. Khi cho học sinh lớp 12 trường THPT Đông Sơn1 tại những lớp tôi giảng dạy làm bài tập “giao thoa ánh sáng có nhiều thành phần đơn sắc” bằng cách chưa phân dạng và chưa xây dựng phương pháp giải kết quả khảo sát thống kê theo bảng 1dưới đây: Bảng 1. Thực trạng khi giải bài tập giao thoa ánh sáng có 3 thành phần đơn sắc của học sinh hai lớp 12 trường THPT Đông Sơn1 năm học 2016 - 2017 Lớp Sĩ số HS giải được HS còn lúng túng HS không biết giải SL TL SL TL SL TL 12A6 46 14 30,4% 18 39,2% 14 30,4% 12A7 44 9 21% 12 27,8% 23 51,2% Qua nhiều năm giảng dạy tôi đã xây dựng cho mình một cách dạy đem lại hiệu quả cao hơn. Bằng cách phân dạng các bài tập và hình thành một phương pháp giải trên cơ sở định hướng, đặt vấn đề để dẫn dắt học sinh tự đúc kết lại cho mình những công thức, áp dụng nhanh khi giải các bài toán trắc nghiệm. 2.3. Các sáng kiến kinh nghiệm đưa ra: 2.3.1. Lý thuyết giao thoa ánh sáng: * Điều kiện để có hiện tượng giao thoa: Là hai nguồn sóng ánh sáng chiếu đến phải là hai nguồn sóng ánh sáng kết hợp. Hai nguồn sóng ánh sáng kết hợp là hai nguồn sáng phát ra hai sóng ánh sáng có cùng bước sóng, hiệu số pha dao động giữa hai nguồn không thay đổi theo thời gian. * Hiện tượng giao thoa: Trong vùng ánh sáng gặp nhau của hai nguồn sáng kết hợp có những vạch sáng xen kẽ những vạch tối gọi là vân giao thoa. Vạch sáng ứng với những vị trí tại đó biên độ sóng được tăng cường, vạch tối ứng với những vị trí biên độ sóng bị triệt tiêu. - Giao thoa của ánh sáng đơn sắc Trong thí nghiệm Y-âng nếu ánh sáng đơn sắc, màn quan sát đặt song song với hai khe thì các vân sáng, vân tối xen kẻ nhau và cách nhau đều đặn, chính giữa màn là vân sáng trung tâm. - Giao thoa ánh sáng có nhiều thành phần đơn sắc Trong thí nghiệm Y-âng, giao thoa ánh sáng khi nguồn sáng gồm nhiều thành phần đơn sác khác nhau, trên màn quan sát đặt song song với hai khe ta quan sát được hệ vân giao thoa như sau: - Chính giữa màn quan sát là vân trung tâm : sự chồng chập của các vân sáng đơn sắc ứng với k = 0 có màu cùng màu với nguồn sáng chiếu đến. Tiếp đến là các vạch sáng màu đơn sắc và những vạch không đơn sắc do có sự chồng chập: + Của các vạch sáng đơn sắc trùng nhau, + Các vạch tối trùng nhau + Hoặc vạch sáng trùng vạch tối giữa các bức xạ . - Với nguồn ánh sáng trắng dải bước sóng từ tím đến đỏ : 0,38 mm £ l £ 0,76 mm Trên màn quan sát ta thấy: + Ở chính giữa là vạch sáng trắng trung tâm. + Tiếp đến là hai vân tối mờ sát hai bên vân trung tâm. + Ở hai bên vân trung tâm, các vân sáng khác của các sóng ánh sáng đơn sắc khác nhau không trùng với nhau nữa, chúng nằm kề sát bên nhau và cho những quang phổ có màu sắc sặc sở giống như màu của đĩa CD ta nhìn ban ngày. + Do tím nhỏ nhất ; itím.= ltím .D/a nhỏ nhất => làm cho tia tím sát với vạch tối mờ (xét cùng một bậc giao thoa). +Tập hợp các vạch từ tím đến đỏ của cùng một bậc (cùng giá trị k) gọi là quang phổ bậc k. * Các công thức của giao thoa ánh sáng: - Vị trí vân sáng: xs = - Vị trí vân tối xt = - Khoảng vân Hay: Vị trí vân sáng : Vị trí vân tối: Trong đó : D là khoảng cách hai khe đến màn a là khoảng cách giữa hai khe là bước sóng ánh sáng dùng trong thí nghiệm k là bậc của vân sáng hoặc thứ của vân tối; k = 0; 2.3.2. Phân dạng và phương pháp giải bài tập “Giao thoa ánh sáng có nhiều thành phần đơn sắc” Trường hợp 1: Nguồn sáng giao thoa có các bức xạ đơn sắc khác nhau Dạng 1. Vị trí các vân trùng nhau: x1 = x2 = x3 D1.1.Vị trí các vân sáng trùng nhau: xs1 = xs2 = xs3 => k1i1 = k2i2 = k3i3 => k1λ1 = k2λ2 = k3λ3 => qk1 = pk2 = p’ k3 Tìm bội chung nhỏ nhất: BSCNN(p,q,p’) = B Cách 1: Tính BCNN bằng cách phân tích thành tích của các thừa số nguyên tố. Cách 2: DÙNG MÁY TÍNH VINA CAL 570ES PLUS MODE 6 2 : (p,q, p’) Lưu ý: Nhập dấu phẩy “,” là phím SHIFT ) và phải nhập số nguyên Vị trí vân sáng trùng nhau: hoặc D1.2. Vị trí hai vân tối trùng nhau của hai bức xạ: + Khi vân tối của 2 bức xạ trùng nhau: (tỉ số tối giản) ; Vị trí trùng hai vân tối: D1.3.Vân sáng của bức xạ này trùng vân tối của bức xạ kia. - Giả sử: (tỉ số tối giản) Vị trí vân sáng trùng với vân tối : x Dạng 2: Khoảng vân trùng : Là khoảng cách ngắn nhất giữa hai vân cùng màu với nhau. Khoảng vân trùng giữa hai vân cùng màu với vân trung tâm. Dạng 3: Số vân trùng quan sát được trong một miền cho trước. D3.1. Số vân trùng quan sát được trên trường giao thoa L: - Cách 1: Tính nhanh bằng máy tính Fx570ES; 570ESPLUS; VINA570ESPLUS: Ta có hàm số f(x) = (Biến số x là n, hàm số f(x) là ) D f(x)= Bước 1: MODE 7 (chọn TABLE ) Bước 2: Nhập hàm số vào máy tính x = n f(x) = x(n) -3 -3,6 -2 -2,4 -1 -1,2 0 0 1 1,2 2 2,4 3 3,6 D Start? 1 Bước 3: bấm = nhập 0 D End? 5 Bước 4: bấm = nhập 5 D Step? 1 Bước 5: bấm = nhập 1 Bước 6: bấm = Ta có bảng biến thiên: f(x). Ví dụ như bảng bên Lấy: --> n tương ứng. Lưu ý: Chọn Start?: Giá trị bắt đầu biến x từ số nguyên âm hay dương(ví dụ: -3). Chọn End?: Kết thúc giá trị biến x. (ví dụ: 4) Chọn Step? : 1 lấy giá trị của biến x là số nguyên. Cách 2: Giải theo toán học thông thường: + Số vân sáng x trong trường giao thoa (1) Mỗi giá trị n1 giá trị ksố vạch sáng trùng là số giá trị n thỏa mãn . + Số vân tối xT trong trường giao thoa: Số vạch trùng quan sát được trên L : D3.2. Số vân trùng quan sát được trên đoạn thuộc trường giao thoaL. (xM < xN; x là tọa độ) khoảng nsố giá trị n là số vân sáng trùng thuộc . Cách 1: Tính nhanh bằng máy tính Fx570ES; 570ESPLUS; VINA570ESPLUS: Dùng MODE 7 (đã nêu mục D3.1 ) Cách 2: Giải theo toán học thông thường: Chú ý: Nếu M,N là vân sáng trùng lấy dấu “ = „. Số vạch trùng quan sát được trên L: ( Nhớ chú ý M,N có phải là vân sáng trùng hay không ) D3.3. Số vân trùng của hai bức xạ trong khoảng giữa hai vân sáng cùng màu với vân trung tâm: Với cặp λ1, λ2 có vân sáng trùng : Với cặp λ2, λ3 có vân sáng trùng : Với cặp λ1, λ3 có vân sáng trùng Tương tự với các cặp vân trùng tiếp theo nếu có thêm các bức xạ nữa. D3.4. Số vân sáng quan sát được trong khoảng giữa hai vân sáng cùng màu với vân trung tâm. Số vân sáng = Tổng số vân sáng tính toán – Số vị trí trùng nhau Số vân sáng đơn sắc = Số vân sáng – Số vị trí trùng nhau Trường hợp 2: Nguồn sáng giao thoa là ánh sáng trắng (0,38 mm £ l £ 0,76 mm) Dạng 1: Các bức xạ của ánh sáng trắng cho vân sáng tại x0 khi: Vị trí vân sáng bất kì x= Vì x=x0 nên: x0 =. với điều kiện:12, Cách 1: Tính nhanh bằng máy tính Fx570ES; 570ESPLUS; VINA570ESPLUS: Dùng MODE 7 (như đã nêu ở mục D3.1) Cách 2: Giải toán thông thường: 1 = 0,38.10-6m (tím)0,76.10-6m =2 (đỏ) Giải hệ bất phương trình trên,, (với kZ) chọn kZ và thay các giá trị k tìm được vào tính với đó là bước sóng các bức xạ của ánh sáng trắng cho vân sáng tại x0. Dạng 2: Các bức xạ của ánh sáng trắng cho vân tối tại x0: Ánh sáng đơn sắc cho vân tối tại vị trí đang xét : Xt = (2k+1)= x0 => f(x) = (k) Cách 1: Tính nhanh bằng máy tính Fx570ES; 570ESPLUS; VINA570ESPLUS Dùng MODE 7 (như đã nêu ở mục D3.1) Cách 2: Giải toán thông thường: Giải toán thông thường với điều kiện :12 12, (với kZ) Thay các giá trị k tìm được vào: đó là bước sóng các bức xạ của ánh sáng trắng cho vân tối tại x0. Dạng 3: Xác định bề rộng quang phổ bậc k khi nguồn sáng giao thoa là ánh sáng trắng Bề rộng quang phổ là khoảng cách giữa vân sáng màu đỏ ngoài cùng và vân sáng màu tím của một vùng quang phổ. xk= xđ- xt = k = k(iđ - it) với k N, k là bậc quang phổ. Bề rộng quang phổ là khoảng cách từ vân sáng đỏ đến vân sáng tím cùng bậc Bề rộng quang phổ bậc 1: Bề rộng quang phổ bậc 2: Bề rộng quang phổ bậc k : x k = x sđk – x stk = k- k. => Bề rộng quang phổ bậc n trong giao thoa với ánh sáng trắng: xk = k. 2.3.3. Bài tập “Giao thoa ánh sáng với nhiều thành phần đơn sắc” 3.3.1. Giao thoa với nguồn ánh sáng gồm hai, ba bức xạ đơn sắc khác nhau. Bài 1: Thực hiện thí nghiệm giao thoa ánh sáng với khe Y-âng. Khoảng cách giữa hai khe là a = 1,6mm. Khoảng cách từ hai khe đến màn là D = 2,4m. Người ta chiếu đồng thời hai bức xạ đơn sắc có bước sóng l1 = 0,45mm và l2 = 0,75 mm. Xác định vị trí trùng nhau thứ 4 của các vân sáng của hai bức xạ l1 và l2 kể từ vân trung tâm. A.10,125mm B. 13,5mm C. 17,5mm D. 20,5mm Giải + Vị trí các vân sáng trùng nhau có tọa độ: Để k1, k2 nguyên thì k1 phải là bội của 5, k2 phải là bội của 3 k1 = 5n, k2 = 3n ( n = 0, 1, 2, 3,...) Vậy tọa độ của các vị trí vân sáng trùng nhau (hay tọa độ các vân cùng màu với vân sáng trung tâm) là: Đáp án A Bài 2: Thí nghiệm Y-âng về giao thoa ánh sáng nguồn phát đồng thời hai bức xạ đơn sắc. λ1 = 0,64μm (đỏ), λ2 = 0,48μm (lam) trên màn hứng vân giao thoa. Trong đoạn giữa 3 vân sáng liên tiếp cùng màu với vân trung tâm có số vân đỏ và vân lam là : A. 9 vân đỏ, 7 vân lam B. 7 vân đỏ, 9 vân lam C. 4 vân đỏ, 6 vân lam D. 6 vân đỏ, 4 vân lam Giải : k1= k2 Hay k1l1 = k2l2 => 4k1=3k2 => Vậy xét vị trí 3 vân trùng màu đầu tiên là (k1; k2) = (3,4) (6;8) và (9;12) Vậy giữa 3 vân sáng liên tiếp cùng màu vân trung tâm có 4 vân đỏ (4,5,7,8) và 6 lam (5,6,7,9,10,11). Đáp án C Bài 3: Trong thi nghiệm Y-âng về giao thoa ánh sáng có a = 2mm, D = 2m. Khi được chiếu bởi ánh sáng có bước sóng thì trên màn quan sát được độ rộng trường giao thoa là 8,1mm. Nếu chiếu đồng thời thêm ánh sáng có thì thấy vân sáng bậc 4 của nó trùng với vân sáng bậc 6 của ánh sáng. Trên màn có số vân sáng trùng nhau quan sát được là x = k f(x)= x(k) -9 -4,5 -8 - 4 -7 -3,5 ... ...... 8 4 9 4,5 A. 7 vân B. 5 vân C. 9 vân D. 3 vân Giải: Cách 1: Dùng máy tính Fx570ES; 570ESPLUS; VINA570ESPLUS : MODE 7 tính nhanh f(x) = x(k) = 0,5k Số vân sáng là: 2.8 + 1 = 17 Cách 2: Giải theo toán học thông thường Đối với bước sóng số vân sáng: Vậy có 17 vân sáng. Vân sáng của và trùng nhau thì Vậy vân sáng trùng nhau ứng với k1=2, 4, 6, 8; 0; -2; -4; -6; -8 => 9 vân trùng => Đáp án C Bài 4: Thực hiện thí nghiệm giao thoa ánh sáng với khe Y-âng. Khoảng cách giữa hai khe là a = 1,6mm. Khoảng cách từ hai khe đến màn là D = 2,4m. Người ta chiếu đồng thời hai bức xạ đơn sắc có bước sóng l1 = 0,45mm và l2 = 0,75 mm. Xác định vị trí vân tối trùng nhau thứ nhất của hai bức xạ l1 và l2. A. 1,6875cm B.1,6875mm C.5,0625mm D. 5,0625cm Giải Vị trí các vân tối trùng nhau: Để k1 nguyên thì (k2 – 1) = 3n ( n = 0, 1, 2, 3,...) Vậy tọa độ của các vị trí vân tối trùng nhau: Vị trí vân tối trùng nhau thứ nhất của hai bức xạ l1 và l2 có n = 0 Xt1= 1,6875mm. Đáp án B Bài 5: Trong thí nghiệm giao thoa Y- âng thực hiện đồng thời hai bức xạ đơn sắc với khoảng vân trên màn thu được lần lượt là: i1 = 0,5mm; i2 = 0,3mm. Biết bề rộng trường giao thoa là 5mm, số vị trí trên trường giao thoa có 2 vân tối của hai bức xạ nói trên trùng nhau là bao nhiêu? A. 2 B.3 C.4 D.5 Giải: x = n f(x) = x(n) -2 -4,5 -1 -1,5 0 1,5 1 4,5 2 7,5 Khi 2 vân tối trùng nhau: Ta có: - Cách 1: Dùng máy tính Fx570ES; 570ESPLUS; VINA570ESPLUS : MODE 7 tính nhanh được bảng sau: => có 4 giá trị n thỏa mãn Cách 2: Giải bất phương trình: có 4 vị trí vân tối trùng nhau trên trường giao thoa L. Đáp án C Bài 6:Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe cách nhau a = 1mm, hai khe cách màn quan sát 1 khoảng D = 2m. Chiếu vào hai khe đồng thời hai bức xạ có bước sóng l1 = 0,4mm và l2 = 0,56mm. Hỏi trên đoạn MN với xM = 10mm và xN = 30mm có bao nhiêu vạch đen của 2 bức xạ trùng nhau? A. 2. B. 5. C. 3. D. 4. Giải: Khoảng vân: i1 = = = 0,8 mm; i2 == =1,12 mm Vị trí hai vân tối trùng nhau: x = (k1+0,5) i1 = (k2 + 0,5)i2 =>(k1+0,5) 0,8 = (k2 + 0,5)1,12 => 5(k1 + 0,5) = 7(k2 + 0,5) => 5k1 = 7k2 + 1 => k1= k2 + ; Để k1 nguyên 2k2 + 1 = 5k => k2 = = 2k + x = n f(x) = x(n) 1 8,4 2 14 3 19,6 4 25,2 5 30,8 Để k2 nguyên k – 1 = 2n => k = 2n +1 với n = 0, 1, 2, .... k2 = 5n + 2 và k1 = k2 + k = 7n + 3 Suy ra x = (7n + 3 + 0,5)i1 = (7n + 3 + 0,5)0,8 = 5,6n + 2,8 10 ≤ x ≤ 30 => 10 ≤ x = 5,6n + 2,8 ≤ 30 Cách 1: Dùng máy tính Fx570ES; 570ESPLUS; VINA570ESPLUS: MODE 7 tính nhanh được bảng sau: Cách 2: Giải bất phương trình: => 2 ≤ n ≤ 4. Có 3 giá trị của n. Đáp án C Bài 7: Trong thí nghiệm giao thoa Y- âng, thực hiện đồng thời với 2 ánh sáng đơn sắc, khoảng vân giao thoa trên màn lần lượt i1 = 0,8mm, i2 = 0,6mm, trường giao thoa rộng: L = 9,6mm. Hỏi số vị trí vân tối của bức xạ 1trùng với vân sáng của bức xạ 2 ta quan sát được trong trường giao thoa là bao nhiêu? . x = n f(x) = x(n) -3 -6 -2 -3,6 -1 -1,2 0 1,2 1 3,6 2 6 A.4 B.5 C. 3 D.2 Giải: => Cách 1: Dùng máy tính Fx570ES; 570ESPLUS; VINA570ESPLUS: MODE 7 tính nhanh được bảng sau: => có 4 giá trị n thỏa mãn Cách 2: Giải bất phương trình: n = 0 ; 1; -1; -2 có 4 giá trị n thỏa mãn Đáp án A Bài 8: Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe a = 2mm, khoảng cách từ hai khe đến màn ảnh D = 2m. Nguồn S phát đồng thời hai bức xạ có bước sóng l1 = 0,5mm và l2= 0,4mm. Trên đoạn MN = 30mm (M và N ở một bên của O và OM = 5,5mm) có bao nhiêu vân tối bức xạ l2 trùng với vân sáng của bức xạ l1? A. 12 B. 15 C. 14 D. 13 Giải: Khoảng vân: i1 = = 0,5 mm; i2 = = 0,4 mm Vị trí vân tối của l2: x2 = (k2+ 0,5) i2 = (k2+ 0,5).0,4 (mm) Vị trí vân sáng của l1: x1 = k1 i1 = 0,5k1 (mm) Vị trí vân tối bức xạ l2 trùng với vân sáng của bức xạ l1: 5,5 (mm) ≤ x2 = x1 ≤ 35,5 (mm) (k2+ 0,5) i2 = k1i1 => 4k2 + 2 = 5k1 => 4k2 = 5k1 – 2=> k2 = k1 +. Để k2 là một số nguyên thị k1 – 2 = 4n ( với n ≥ 0) Do đó k1 = 4n + 2 và k2 5n + 2; x = n f(x) = x(n) 2 5 3 7 4 9 16 33 17 35 18 37 Khi đó x1 = 0,5k1 = 2n + 1 5,5 (mm) ≤ x1 = 2n + 1 ≤ 35,5 (mm) Cách 1: Dùng máy tính Fx570ES; 570ESPLUS; VINA570ESPLUS: MODE 7 tính nhanh được bảng sau: Cách 2: Giải bất phương trình: => 3 ≤ n ≤ 17 Trên đoạn MN có 15 vân tối bức xạ l2 trùng với vân sáng của bức xạ l1. Đáp án B Bài 9: Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu đồng thời 3 bức xạ đơn sắc có bước sóng : λ1 = 0,4μm, λ2 = 0,5μm, λ3 = 0,6μm. Trên màn quan sát ta hứng được hệ vân giao thoa, trong khoảng giữa hai vân sáng gần nhau nhất cùng màu với vân sáng trung tâm, ta quan sát được bao nhiêu vân sáng? A. 34 B.32 C. 31 D.27 Giải: Khi các vân sáng trùng nhau: k1λ1 = k2λ2 = k3λ3 k10,4 = k20,5 = k30,6 4k1 = 5k2 = 6k3 Cách 1: Tính BCNN bằng cách phân tích thành tích của các thừa số nguyên tố. Cách 2: DÙNG MÁY TÍNH VINA CAL 570ES PLUS MODE 6 2 : (p,q, p’) BSCNN(4,5,6) = 60=> k1 = 15 ; k2 = 12 ; k3 = 10 : Bậc 15 của λ1 trùng bậc 12 của λ2 trùng với bậc 10 của λ3 Trong khoảng giữa hai vân sáng gần nhau nhất cùng màu với vân sáng trung tâm có: + Tổng số vân sáng tính toán = 14 + 11 + 9 = 34 vân Ta lập tỉ số cho tới khi k1 = 15 ; k2 = 12 ; k3 = 10 - Với cặp λ1, λ2 : : trong khoảng giữa có 2 vị trí trùng nhau( k1 =5; 10). - Với cặp λ2, λ3 : : trong khoảng giữa có 1 vị trí trùng nhau.( k2 =6). - Với cặp λ1, λ3 : : trong khoảng giữa có 4 vị trí trùng nhau.( k3 = 2; 4; 6; 8) Vậy tất cả có 2 + 1 +4 =7 vị trí trùng nhau của các bức xạ. Số vân sáng quan sát được = Tổng số vân sáng tính toán – Số vị trí trùng nhau = 34 – 7 = 27 vân sáng. Đáp án D Bài 10 Trong thí nghiệm Y-âng về giao thoa ánh sáng. Lần thứ nhất, ánh sáng dùng trong thí nghiệm có 2 loại bức xạ 1 = 0,56và bức xạ đỏ với, thì trong khoảng giữa hai vạch sáng gần nhau nhất cùng màu với vạch sáng trung tâm có 6 vân sáng màu đỏ. Lần thứ 2, ánh sáng dùng trong thí nghiệm có 3 loại bức xạ 1, và3 với, khi đó trong khoảng giữa 2 vạch sáng gần nhau nhất và cùng màu với vạch sáng trung tâm còn có bao n
Source: https://thomaygiat.com
Category : Nghe Nhìn

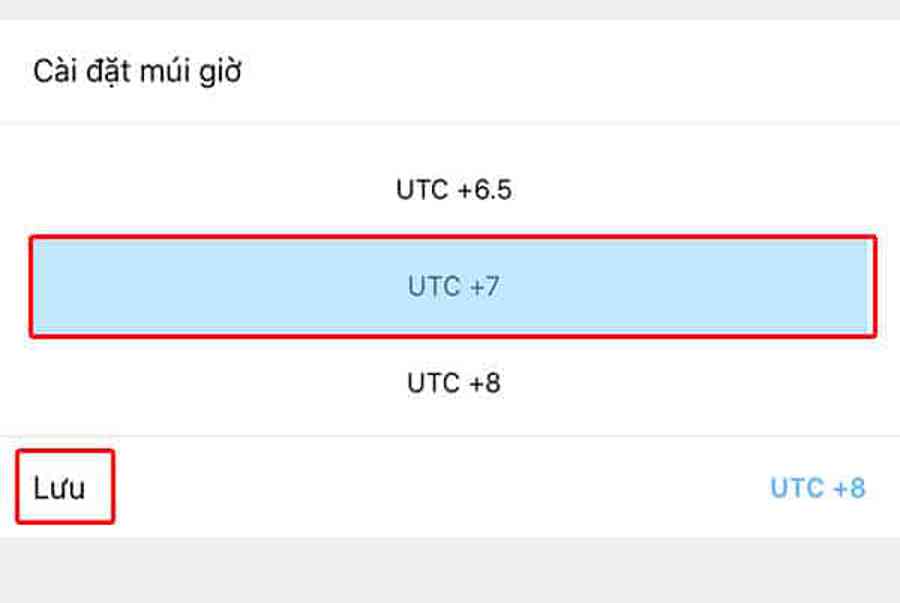
Cách SỬA LỖI CAMERA YOOSEE đơn giản NHẤT [2023]
Mục ChínhVideo cách sửa lỗi camera yoosee không liên kết được wifiCamera Yoosee Không Xoay ĐượcCamera Yoosee bị Sai Giờ Lỗi camera Yoosee báo mạng…

Camera IP Quan Sát Không Dây YooSee 4 Râu C12
Camera IP Quan Sát Không Dây YooSee 4 Râu C12 Camera IP Yosee hạng sang chính hãng model C12 với chất lượng hình ảnh cao…

Camera Wifi Không dây Yoosee HD 3 Râu 1080p – Yoosee Việt Nam
Khả năng xoay linh hoạt dễ dàng quan sát Camera giám sát với khả năng xoay ngang 355°, xoay dọc 120° giúp người dùng dễ dàng…

Cáp Đồng Trục Liền Nguồn Việt Hàn RG59-Cu 1.0 – Chính Hãng
Cáp đồng trục liền nguồn Việt Hàn RG59-Cu 1.0 – cáp lõi đồng nguyên chất, chất lượng cao, giá tốt chính hãng Cáp đồng trục…

Lắp Đặt Camera Lùi Cho Xe Tải – Bảo Việt Technology
Bạn đang đọc: Lắp Đặt Camera Lùi Cho Xe Tải – Bảo Việt Technology 4.4 / 5 – ( 23 bầu chọn ) Doanh nghiệp…

Camera Logo Design PNG Picture, Camera Logo Design Free Logo Design Template, Logo, Flat, Shot PNG Image For Free Download
Successfully saved Free tải về HD contents without watermark please go to pngtree.com via PCOK Bạn đang đọc: Camera Logo Design PNG Picture, Camera Logo…
![Thợ Sửa Máy Giặt [ Tìm Thợ Sửa Máy Giặt Ở Đây ]](https://thomaygiat.com/wp-content/uploads/sua-may-giat-lg-tai-nha-1.jpg)
