Chứng Minh Mạch Cầu Cân Bằng – Minh Gà Chọi

Mạch cầu điện trở là một dạng bài tập khó nhất chương dòng điện không đổi. Bài viết trình bày phương pháp giải bài tập và các bài tập có lời giải chi tiết để bạn đọc tự luyện.Bạn đang xem: Mạch cầu cân bằng là gì

TÍNH ĐIỆN TRỞ MẠCH CẦU KHI BIẾT CÁC GIÁ TRỊ ĐIỆN TRỞ CONMạch cầu tổng quát
I, mạch cầu cân bằng :

– hi đặt một hiệu điện thế UAB khác 0 thì ta nhận thấy I5 = 0.

Bạn đang xem : Chứng minh mạch cầu cân bằng
– Đặc điểm của mạch cầu cân bằng .
+ Ta hoàn toàn có thể vẽ lại mạch gồm : ( R1 / / R3 ) nt ( R2 / / R4 ) hoặc ( R1 nt R2 ) / / ( R3 nt R4 )
+ Về điện trở ( frac { R_ { 1 } } { R_ { 2 } } = frac { R_ { 3 } } { R_ { 4 } } Leftrightarrow frac { R_ { 1 } } { R_ { 3 } } = frac { R_ { 2 } } { R_ { 4 } } )
+ Về dòng điện : I1 = I2 ; I3 = I4 Hoặc ( frac { I_ { 1 } } { I_ { 3 } } = frac { R_ { 3 } } { R_ { 1 } } ; frac { I_ { 2 } } { I_ { 4 } } = frac { R_ { 4 } } { R_ { 2 } } )

+ Về hiệu điện thế: U1 = U3; U­2 = U4 Hoặc ( frac{U_{1}}{U_{2}}=frac{R_{1}}{R_{2}};frac{U_{3}}{U_{4}}=frac{R_{3}}{R_{4}}) 

Bài 1: Cho mạch điện như hình vẽ. Với R1=1Ω, R2=2Ω, R3=3Ω, R4= 6Ω, R5 = 5Ω. UAB=6V. Tính I qua các điện trở?

Giải:

Ta có : ( frac { R_ { 1 } } { R_ { 2 } } = frac { R_ { 3 } } { R_ { 4 } } ) ( rightarrow ) Mạch AB là mạch cầu cân bằng ( rightarrow ) I5 = 0. ( Bỏ qua R5 ) .
Mạch điện tương tự : ( R1 nt R2 ) / / ( R3 nt R4 )
– Cường độ dòng điện qua những điện trở
I1 = I2 = ( frac { U_ { AB } } { R_ { 1 } + R_ { 2 } } = frac { 6 } { 1 + 2 } = 2A ) ; I3 = I4 = ( frac { U_ { AB } } { R_ { 3 } + R_ { 4 } } = frac { 6 } { 3 + 6 } approx 0,67 A )

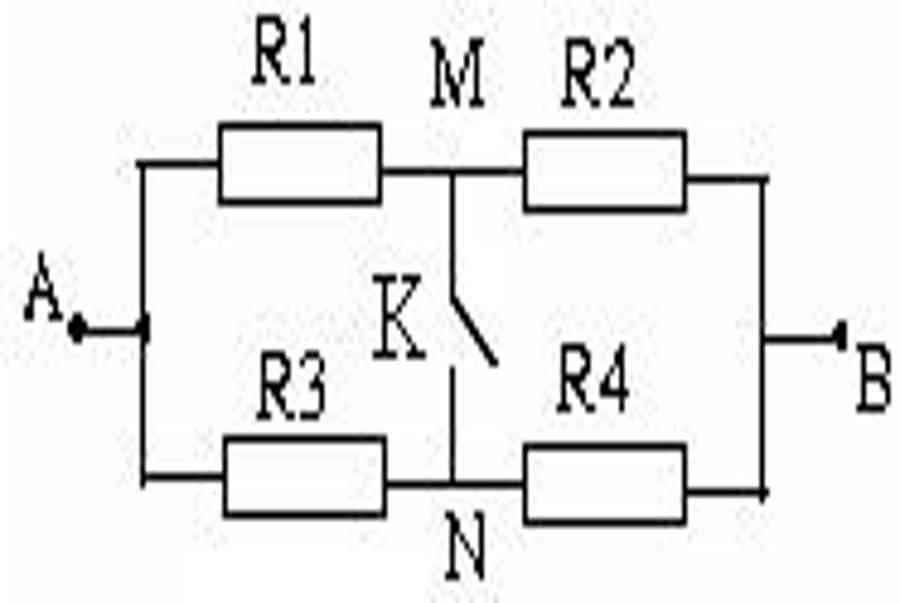
Bài 2: Cho mạch điện mắc như hình vẽ bên:

Chứng minh rằng nếu có :
( frac { R_ { 1 } } { R_ { 2 } } = frac { R_ { 3 } } { R_ { 4 } } Leftrightarrow frac { R_ { 1 } } { R_ { 3 } } = frac { R_ { 2 } } { R_ { 4 } } )
Thì khi K đóng hay K mở, điện trở tương tự của bộ tụ đều không đổi khác .

Bài 3: Cho 12 điện trở được ghép thành mạch như hình vẽ.

Tính điện trở tương tự của cả đoạn mạch .
Với R1 = R5 = R9 = R4 = 1 ( Omega ) ,
R3 = R6 = R10 = R12 = 2 ( Omega ), R2 = 3 ( Omega ) ,
R8 = 4 ( Omega ), R7 = 6 ( Omega ), R11 = 2 ( Omega ) .

Bài 4: Tính điện trở tương đương của mạch:

II, Mạch cầu không cân bằng:

– Khi đặt một hiệu điện thế UAB khác 0 thì ta nhận thấy I5 khác 0 .

 Bài 1: Cho mạch điện như hình vẽ:

Tính điện trở tương tự của mạch điện .
Xem thêm : Những Bài Hát Hay Nhất Của Hữu Thọ : Giọng Ca Trữ Tình Chinh Phục Nhiều Thế Hệ
Lưu ý :
* Cách 1, 2, 3 có sử dụng 2 định luật Kirchhoff như sau :
( hoàn toàn có thể tìm được tư liệu về định luật này ở nhiều sách nâng cao. Các công thức này hoàn toàn có thể tự chứng minh theo ý hiểu cá thể, nhưng mình sẽ lấy cái tổng quát nhất là dựa vào định luật Kirchhoff )
+ Nếu dòng điện đi từ M đến N :

Tại nút N ta có : I4 = I5 + I3Tại nút M ta có : I1 = I2 + I5
Tại mắt mạng AMN : U1 + U5 = U3
Tại mắt mạng MNB : U4 + U5 = U2
U5 = VM – việt nam
+ Nếu dòng điện đi từ N đến M :
Tại nút M ta có : I1 = I2 – I5

 Tại mắt mạng AMN: U1 – U5 = U3Tại nút N ta có: I4 = I3 – I5

Tại mắt mạng MNB : U4 – U5 = U2
U5 = việt nam – VM
* Bình thường 1 số ít bài toán không cho dấu của 2 cực của nguồn ( điều này không tác động ảnh hưởng đến đáp án ) ta vẫn phải làm thao tác “ giả sử chiều dòng điện như hình vẽ ”. Thao tác này vừa để chọn chiều dòng điện qua MN vừa để chọn dấu của 2 cực của nguồn. Các công thức trên mình đều chọn cực dương ở A, cực âm ở B và khi giải bài toán này mình vẫn chọn như vậy. ( Nếu chọn cực âm ở A, cực dương ở B thì chỉ việc hòn đảo chỗ những công thức ở 2 trường hợp cho nhau )

Giải:

 Cách 1. đặt ẩn là hiệu điện thế

-Phương pháp chung.

+ Giả sử chiều dòng điện từ M đến N.

+ Chọn 2 hiệu điện thế bất kỳ làm 2 ẩn .
+ Sau đó qui những hiệu điện thế còn lại theo ẩn đã chọn .
+ Giải bài theo ẩn đó .

VD ta chọn 2 ẩn là U1 và U3.

Giả sử chiều dòng điện như hình vẽ ( hình α )
Ta có : I1 = ( frac { U_ { 1 } } { R_ { 1 } } ), I3 = ( frac { U_ { 3 } } { R_ { 3 } } ) ,
U1 + U5 = U3 ( rightarrow ) U5 = U3 – U1 ( rightarrow ) I5 = ( frac { U_ { 5 } } { R_ { 5 } } = frac { U_ { 3 } – U_ { 1 } } { R_ { 5 } } ) I2 = I1-I5 ( rightarrow ) I2 = ( frac { U_ { 1 } } { R_ { 1 } } – frac { U_ { 3 } – U_ { 1 } } { R_ { 5 } } )
( rightarrow ) U2 = I2. R2 = ( ( frac { U_ { 1 } } { R_ { 1 } } – frac { U_ { 3 } – U_ { 1 } } { R_ { 5 } } ) ). R2
I4 = I3 + I5 ( rightarrow ) I4 = ( frac { U_ { 3 } } { R_ { 3 } } + frac { U_ { 3 } – U_ { 1 } } { R_ { 5 } } ) ( rightarrow ) U4 = I4. R4 = (. ( frac { U_ { 3 } } { R_ { 3 } } + frac { U_ { 3 } – U_ { 1 } } { R_ { 5 } } ) ). R4
Lại có : UC = U1 + U2 = U3 + U4 ( Leftrightarrow ) U1. ( 1 + ( frac { R_ { 2 } } { R_ { 2 } } + frac { R_ { 2 } } { R_ { 5 } } ) ) – U3. ( frac { R_ { 2 } } { R_ { 5 } } ) = U3. ( 1 ( + frac { R_ { 4 } } { R_ { 3 } } + frac { R_ { 4 } } { R_ { 5 } } ) ) – U1. ( frac { R_ { 4 } } { R_ { 5 } } )
( Leftrightarrow ) U1 ( 1 ( + frac { R_ { 2 } } { R_ { 2 } } + frac { R_ { 2 } } { R_ { 5 } } + frac { R_ { 4 } } { R_ { 5 } } ) ) = U3. ( 1 ( + frac { R_ { 4 } } { R_ { 3 } } + frac { R_ { 4 } } { R_ { 5 } } + frac { R_ { 2 } } { R_ { 5 } } ) )
( Leftrightarrow ) U1 = ( frac { 1 + frac { R_ { 2 } } { R_ { 2 } } + frac { R_ { 2 } } { R_ { 5 } } + frac { R_ { 4 } } { R_ { 5 } } } { 1 + frac { R_ { 4 } } { R_ { 3 } } + frac { R_ { 4 } } { R_ { 5 } } + frac { R_ { 2 } } { R_ { 5 } } } ) U3 ( rightarrow ) UC = U1 + U2 = …. ( rightarrow ) PHỨC TẠP

*VD ta chọn 2 ẩn là U1 và U2.

Ta có : I1 = ( frac { U_ { 1 } } { R_ { 1 } } ), I2 = ( frac { U_ { 2 } } { R_ { 2 } } ) ( rightarrow ) I5 = I1 – I2 ( rightarrow ) I5 = ( frac { U_ { 1 } } { R_ { 1 } } ) – ( frac { U_ { 2 } } { R_ { 2 } } ) ( rightarrow ) U5 = I5. R5 = ( ( frac { U_ { 1 } } { R_ { 1 } } ) – ( frac { U_ { 2 } } { R_ { 2 } } ) ). R5
Lại có :
U1 + U5 = U3 ( rightarrow ) U3 = U1 + U5 = U1 + ( ( frac { U_ { 1 } } { R_ { 1 } } ) – ( frac { U_ { 2 } } { R_ { 2 } } ) ). R5 ( rightarrow ) I3 = frac { U_ { 3 } } { R_ { 3 } } ) = ( frac { 1 } { 3 } ) U1 + ( frac { 5 } { 3 } ) U1 – ( frac { 5 } { 6 } ) U2 = 2U1 – ( frac { 5 } { 6 } ) U2
U5 + U4 = U2 ( rightarrow ) U4 = U2 – U5 = U2 – ( ( frac { U_ { 1 } } { R_ { 1 } } ) – ( frac { U_ { 2 } } { R_ { 2 } } ) ). R5 ( rightarrow ) I4 = ( frac { U_ { 4 } } { R_ { 4 } } ) = ( frac { 1 } { 4 } ) U2 – ( frac { 5 } { 4 } ) U1 + ( frac { 5 } { 8 } ) U2 = ( frac { 7 } { 8 } ) U2 – ( frac { 5 } { 4 } ) U1
Mà : IC = I1 + I3 = I2 + I4 ( Leftrightarrow ) U1 + 2U1 – ( frac { 5 } { 6 } ) U2 = ( frac { 1 } { 2 } ) U2 + ( frac { 7 } { 8 } ) U2 – ( frac { 5 } { 4 } ) U1
( Leftrightarrow ) ( frac { 17 } { 4 } ) U1 = ( frac { 53 } { 24 } ) U2 ( Leftrightarrow ) U1 = ( frac { 53 } { 102 } ) U2
→ UC = U1 + U2 = ( frac { 155 } { 102 } ) U2, IC = I1 + I3 = 3U1 – ( frac { 5 } { 6 } ) U2 = ( frac { 37 } { 51 } ) U2
→ RTĐ = ( frac { U_ { c } } { I_ { c } } = frac { 155 } { 74 } Omega )

NHẬN XÉT: ĐIỀU NÀY CHO THẤY VIỆC ĐẶT ẨN SAO CHO PHÙ HỢP SẼ GIÚP RÚT NGẮN THỜI GIAN LÀM BÀI.

 Cách 2. Đặt ẩn là dòng

– Phương pháp chung.

+ Giả sử chiều dòng điện từ M đến N.

+ Chọn 2 dòng bất kể làm ẩn .
Xem thêm : Trinh Đinh Quang Official – Page Not Found và Bull Instagram
+ Giải bài theo ẩn đó .

VD: ta chọn 2 ẩn là I1, I3.

Ta có : U1 = I1. R1, U3 = I3. R3
Lại có : U1 + U5 = U3 → U5 = U3 – U1 = I3. R3 – I1. R1 → I5 ( frac { I_ { 3 }. R_ { 3 } – I_ { 1 }. R_ { 1 } } { R_ { 5 } } = frac { 3I _ { 3 } – I_ { 1 } } { 5 } )
ð I2 = I1 – I5 = I1 – ( frac { 3I _ { 3 } – I_ { 1 } } { 5 } ) = ( frac { 6 } { 5 } ) I1 – ( frac { 3 } { 5 } ) I3 → U2 = I2. R2 = ( frac { 12 } { 5 } ) I1 – ( frac { 6 } { 5 } ) I3

 I4 = I3 + I5 = I3 + ( frac{3I_{3}-I_{1}}{5}) = ( frac{8}{5}) I3 – ( frac{1}{5})I1 → U4 = I4.R4 = ( frac{32}{5})I3 – (frac{4}{5}) I1

Mà : UC = U1 + U2 = U3 + U4 ( Leftrightarrow ) I1 + ( frac { 12 } { 5 } ) I1 – ( frac { 6 } { 5 } ) I3 = 3I3 + ( frac { 32 } { 5 } ) I3 – ( frac { 4 } { 5 } ) I1
( Leftrightarrow ) ( frac { 21 } { 5 } ) I1 = ( frac { 53 } { 5 } ) I3 ( Leftrightarrow ) I1 = ( frac { 53 } { 21 } ) I3
( Rightarrow ) IC = I1 + I3 = ( frac { 74 } { 21 } ) I3, UC = U1 + U2 = I1 + ( frac { 12 } { 5 } ) I1 – ( frac { 6 } { 5 } ) I3 = ( frac { 155 } { 21 } ) I3

Source: https://thomaygiat.com
Category : Điện Tử