Định luật Kirchhoff – Wikipedia tiếng Việt

” Định luật Kirchhoff ” đổi hướng tới đây. Đối với những định nghĩa khác, xem Định luật Kirchhoff ( xu thế )

Trong mạch điện, định luật Kirchhoff là hai phương trình để mô tả mối quan hệ của cường độ dòng điện và điện áp. Các định luật này được Gustav Kirchhoff xây dựng vào năm 1845.[1]

Định luật Kirchhoff về cường độ dòng điện[sửa|sửa mã nguồn]

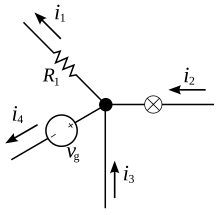i2 + i3 = i1 + i4Với qui ước: Dòng điện rời khỏi nút có giá trị âm và dòng điện hướng vào nút có giá trị dương (hay ngược lại).Dòng điện vào nút bằng dòng điện từ nút ra. Với qui ước : Dòng điện rời khỏi nút có giá trị âm và dòng điện hướng vào nút có giá trị dương ( hay ngược lại ) .

Định luật này còn được gọi là định luật Kirchhoff 1 (K1) hay định luật bảo toàn điện tích tại một nút, gọn lại là định luật nút.

Nguyên lý về bảo toàn điện tích bao hàm ý :

Tại bất kỳ nút (ngã rẽ) nào trong một mạch điện, thì tổng cường độ dòng điện chạy đến nút phải bằng tổng cường độ dòng điện từ nút chạy đi, hay:

Tổng giá trị đại số của dòng điện tại một nút trong một mạch điện là bằng không.

Công thức :

∑ k = 1 n I k = 0 { \ displaystyle \ sum _ { k = 1 } ^ { n } { I } _ { k } = 0 }

với n là tổng số các nhánh với dòng điện chạy vào nút hay từ nút ra.

Công thức theo dòng phức :

∑ k = 1 n I ~ k = 0 { \ displaystyle \ sum _ { k = 1 } ^ { n } { \ tilde { I } } _ { k } = 0 }

Định luật Kirchhoff về điện thế[sửa|sửa mã nguồn]

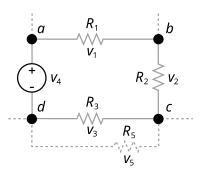1 + v2 + v3 – v4 = 0Tổng của những điện áp quanh vòng kín là không. v + v + v – v = 0Định luật này còn gọi là định luật Kirchhoff 2 ( K2 ) hay định luật bảo toàn điện áp trong một vòng, gọn lại là định luật vòng kín .Cũng như định luật K1, định luật K2 phát biểu :

Tổng giá trị điện áp dọc theo một vòng bằng 0.

Công thức :

∑ k = 1 n V k = 0 { \ displaystyle \ sum _ { k = 1 } ^ { n } V_ { k } = 0 }

với n là tổng số các điện áp được đo.

Công thức theo điệp áp phức :

∑

k
=
1

n

V
~

k

=
0

{\displaystyle \sum _{k=1}^{n}{\tilde {V}}_{k}=0}

Xem thêm: Quy ước chiều dòng điện là?

Ví dụ mạch gồm 3 điện trở và 2 nguồn như hình :

Theo định luật 1, ta có :

− i 1 + i 2 + i 3 = 0 { \ displaystyle – i_ { 1 } + i_ { 2 } + i_ { 3 } = 0 \, }

Định luật 2 áp dụng cho vòng s1:

R 2 i 2 − ϵ 1 + R 1 i 1 = 0 { \ displaystyle R_ { 2 } i_ { 2 } – \ epsilon _ { 1 } + R_ { 1 } i_ { 1 } = 0 }

Định luật 2 áp dụng cho vòng s2:

R 3 i 3 + ϵ 2 + ϵ 1 − R 2 i 2 = 0 { \ displaystyle R_ { 3 } i_ { 3 } + \ epsilon _ { 2 } + \ epsilon _ { 1 } – R_ { 2 } i_ { 2 } = 0 }

Đến đây ta có hệ phương trình tuyến tính cho 3 ẩn số

i

1

,

i

2

,

i

3

{\displaystyle i_{1},i_{2},i_{3}}

:

{ − i 1 + i 2 + i 3 = 0 R 2 i 2 − ϵ 1 + R 1 i 1 = 0 R 3 i 3 + ϵ 2 + ϵ 1 − R 2 i 2 = 0 { \ displaystyle { \ begin { cases } – i_ { 1 } + i_ { 2 } + i_ { 3 } và = 0 \ \ R_ { 2 } i_ { 2 } – \ epsilon _ { 1 } + R_ { 1 } i_ { 1 } và = 0 \ \ R_ { 3 } i_ { 3 } + \ epsilon _ { 2 } + \ epsilon _ { 1 } – R_ { 2 } i_ { 2 } và = 0 \ \ \ end { cases } } }

Giả sử :

R 1 = 100, R 2 = 200, R 3 = 300 ( ohm ) ; ϵ 1 = 3, ϵ 2 = 4 ( volt ) { \ displaystyle R_ { 1 } = 100, \ R_ { 2 } = 200, \ R_ { 3 } = 300 { \ text { ( ohm ) } } ; \ \ epsilon _ { 1 } = 3, \ \ epsilon _ { 2 } = 4 { \ text { ( volt ) } } }

hiệu quả :

{

i

1

=

1
1100

 hay 

0.

90
¯

 mA

i

2

=

4
275

 hay 

14.

54
¯

 mA

i

3

=
−

3
220

 hay 

−
13.

63
¯

 mA

{\displaystyle {\begin{cases}i_{1}={\frac {1}{1100}}{\text{ hay }}0.{\bar {90}}{\text{ mA}}\\i_{2}={\frac {4}{275}}{\text{ hay }}14.{\bar {54}}{\text{ mA}}\\i_{3}=-{\frac {3}{220}}{\text{ hay }}-13.{\bar {63}}{\text{ mA}}\\\end{cases}}}

Xem thêm: Sửa Tivi Sony Huyện Thanh Trì

i

3

{\displaystyle i_{3}}

mang dấu âm vì hướng của

i

3

{\displaystyle i_{3}}

ngược với hướng giả định trong hình.

1. ^

   Oldham, Kalil T. Swain (2008). The doctrine of description: Gustav Kirchhoff, classical physics, and the “purpose of all science” in 19th-century Germany (Ph. D.). University of California, Berkeley. tr. 52. Docket 3331743. 3331743.

Liên kết ngoài[sửa|sửa mã nguồn]

• MIT video lecture on the KVL and KCL methods

Source: https://thomaygiat.com
Category : Điện Tử