Các phần tử và mạch logic khí – Real Group
Mục Chính
1. Một số hàm logic cơ bản
1.1. Hàm AND
Xét hàm AND có n cửa vào 1, 2, …, n. Hàm này thực hiện phép toán sau :
Out = (In1) AND (In2) AND … AND (Inn)
Có nghĩa là cửa ra chỉ được kích thích khi tổng thể n cửa vào đều được kích thích .
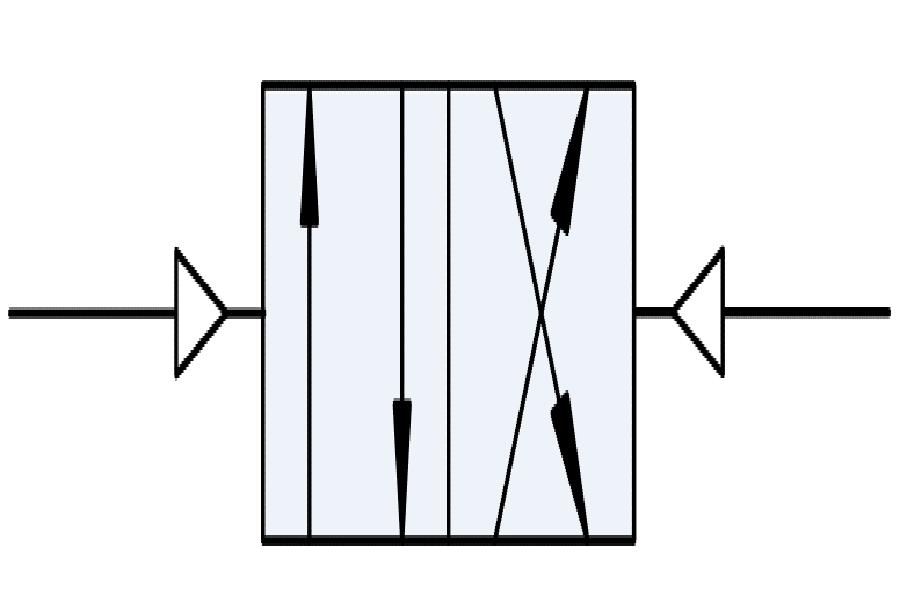
Hàm logic khí AND:
Bạn đang đọc: Các phần tử và mạch logic khí – Real Group

1.2. Hàm OR
Xét hàm OR có n cửa vào 1, 2, …, n. Hàm này thực hiện phép toán sau :
Out = (In1) OR (In2) OR … OR (Inn)
Có nghĩa là cửa ra được kích thích khi chỉ cần 1 cửa vào được kích thích .
Hàm logic khí OR :

1.3. Hàm NOT
Hàm này luôn chỉ có 1 tín hiệu vào .
Khi không có xung tinh chỉnh và điều khiển thì tín hiệu ra bằng tín hiệu vào, khi có xung điều khiển và tinh chỉnh Open thì tín hiệu ra mất .

1.4. Hàm NAND
Xét hàm NAND có n cửa vào 1, 2, …, n. Hàm này thực hiện phép toán sau :
Out = (In1) NAND (In2) NAND … NAND (Inn)
Có nghĩa là cửa ra chỉ không được kích thích khi tổng thể cửa vào được kích thích .
Để minh họa, ta xét hàm NAND có 2 cửa vào In1, In2. Bảng thực sự cho hàm này như sau :
| In1 | In2 | OUT |
| không | không | có |
| không | có | có |
| có | không | có |
| có | có | không |
1.5. Hàm NOR
Xét hàm NOR có n cửa vào 1, 2, …, n. Hàm này thực hiện phép toán sau :
Out = (In1) NOR (In2) NOR … NOR (Inn)
Có nghĩa là cửa ra chỉ được kích thích khi tổng thể cửa vào không được kích thích .
Để minh họa, ta xét hàm NOR có 2 cửa vào In1, In2. Bảng thực sự cho hàm này như sau :
| In1 | In2 | OUT |
| không | không | có |
| không | co | không |
| có | không | không |
| có | có | không |
1.6. Hàm có nhớ
Xung điều khiển và tinh chỉnh ở cửa thứ 1 sẽ duy trì tín hiệu ra cho đến khi Open xung tinh chỉnh và điều khiển ở cửa thứ 2 .

1.7 Hàm có nhớ giới hạn
Khi có xung tinh chỉnh và điều khiển, cửa ra nhận tín hiệu của cửa vào và chỉ duy trì trong 1 khoảng chừng thời hạn xác lập .

2. Số nhị phân
Trong mạng lưới hệ thống tinh chỉnh và điều khiển khí, chỉ có 2 trạng thái hoàn toàn có thể có của van và 2 vị trí hoàn toàn có thể có của xy-lanh .
Vì vậy, tổng thể những trạng thái của phần tử khí hoàn toàn có thể trình diễn bởi mã nhị phân ; trong đó :
- 0 biểu diễn trạng thái OFF.
- 1 biểu diễn trạng thái ON của van hoặc tiếp điểm.
Việc dùng số nhị phân diễn đạt mạch khí được cho phép tối giản mạch khí và đơn giản hóa việc làm thiết kế .
3. Đại số Boole
Đại số Boole là những phép tính dựa trên 2 chữ số 0 và 1 .
Đại số Boole chỉ tương quan đến 2 trạng thái hoàn toàn có thể có của tín hiệu :
- “đúng” hoặc “sai”,
- “ON” hoặc “OFF”,
- “1” hoặc “0”,
- “vào” hoặc “ra”, …
4. Các phần tử logic khí và ứng dụng của đại số Boole
Để thuận tiện cho việc vận dụng đại số Boole vào mạng lưới hệ thống khí, tất cả chúng ta đưa ra 1 số ít ký hiệu sau :
- Tín hiệu vào hoặc ra được biểu thị bằng chữ cái hoặc giá trị số. Khi biểu diễn bằng giá trị số có nghĩa là giá trị của nó không thay đổi.
- OR có thể biểu diễn bởi (+) hoặc ∪ hoặc V.
- AND có thể biểu diễn bới dấu (•) hoặc ∩ hoặc Λ.
- Gạch ngang trên đầu các chữ cái biểu thị trạng thái đảo.
Sau đây là một số ít hàm logic đại số Boole thông dụng :

Bảng tóm tắt các hàm logic và bảng sự thật
Xem thêm: Sửa Tivi Sony Quận Đống Đa










5. Một số ví dụ về phương trình điều khiển
Ví dụ 1: Một hệ thống đưa nguyên liệu vào máy dập có thể hoạt động bằng tay hoặc tự động với các điều kiện đầu như sau:
- Vật cần nén phải vào đúng vị trí.
- Vật đó phải được kẹp lại.
- Không có bộ phận nào của cơ thể người vận hành nằm trong phạm vi làm việc của máy.
Gọi :
- A1 là công tắc hoạt động tay;
- A2 là công tắc hoạt động tự động;
- B1 là cảm biến vị trí đặt của vật;
- B2 là cảm biến kẹp;
- C là tay người vận hành;
- Y là tín hiệu ra.
 Hình 1. Sơ đồ điều khiển logic.
Hình 1. Sơ đồ điều khiển logic.
 Hình 2. Mạch khí nén.
Hình 2. Mạch khí nén.
Ví dụ 2: Một xy-lanh tác động đơn được điều khiển hành trình ra từ 1 trong 2 vị trí A, B khác nhau. Hãy thiết kế mạch điều khiển theo yêu cầu.
Gọi :
- Y là tín hiệu ra tới van điều khiển xy-lanh.
- A, B là hai van điều khiển hướng.
 Hình 3. Sơ đồ diều khiển logic.
Hình 3. Sơ đồ diều khiển logic.
 Hình 4. Mạch khí nén.
Hình 4. Mạch khí nén.
6. Sử dụng bảng Karnaugh-Veitch để thiết kế mạch khí
6.1 Biểu đồ Karnaugh-Veitch
Biểu đồ Karnaugh-Veitch ( K-V ) được sử dụng thoáng rộng để đơn giản hóa những bài toán tinh chỉnh và điều khiển phức tạp .
trái lại với biểu đồ Venn chỉ màn biểu diễn biểu đồ những biến điều khiển và tinh chỉnh và tạo ra phương trình đại số dưới dạng đại số Boole, biểu đồ Karnaugh-Veitch đưa ra một cách tốt hơn và đơn thuần hơn về trạng thái và những mối quan hệ giữa những tín hiệu tinh chỉnh và điều khiển .
Những biểu đồ Karnaugh-Veitch này hoàn toàn có thể gồm có một lượng rất lớn những biến tinh chỉnh và điều khiển dưới dạng đại số và logic nhị phân .
Từ biểu đồ này, thiết lập những phương trình sau đó dùng biểu đồ tối thiểu hóa chúng dựa vào những luật cơ bản của đại số tập hợp để sau cùng thu được phương trình tinh chỉnh và điều khiển ở dạng đơn thuần nhất .
Ưu điểm lớn nhất của biểu đồ Karnaugh-Veitch là ở chỗ chúng có năng lực chuyển những biến dưới dạng toán logic YES / NO vào một bảng gồm nhiều ô và trong mỗi ô lưu lại sự xuất hiện hay không xuất hiện của biến .
Hình minh họa biểu đồ Karnaugh-Veitch cho một biến tinh chỉnh và điều khiển A, gồm 2 ô A và, hoàn toàn có thể dùng số “ 1 ” để trình diễn trạng thái A và “ 0 ” để màn biểu diễn trạng thái A .

Hình trên trình diễn cho hàm 2 biến A và B gồm 22 = 4 ô ; cách chuyển những giá trị trong bảng thực sự vào biểu đồ Karnaugh-Veitch. Phương trình tinh chỉnh và điều khiển được tạo ra bởi những ô có giá trị là “ 1 ” .

Biểu đồ K-V cho hàm ba biến A, B và C :

6.2 Thiết kế mạch khí với biểu đồ Karnaugh-Veitch
Xét 2 xy-lanh A và B được điều khiển và tinh chỉnh theo chuỗi để kẹp và dập một vật thể .
Để sử dụng được kỹ thuật biểu đồ Karnaugh-Veitch trong thiết kế mạch, tất cả chúng ta phải biết cách sử dụng sơ đồ bước vị trí như trên hình vẽ .

- a) Sơ đồ bước vị trí của các xy-lanh.
- b) Biểu đồ hướng và dòng tín hiệu.
- c) Đường biểu diễn lưu lượng và đường tín hiệu.
Biểu đồ Karnaugh-Veitch với hướng và dòng tín hiệu

Để tối thiểu hóa phương trình logic trên, phải vẽ những biểu đồ Karnaugh-Veitch riêng cho mỗi trạng thái nhớ, tức là với A1, A0, B1, B0, X1, X0, …
Chẳng hạn với van điều khiện hướng của A, sự hiện hữu của A1 và A0 được vẽ trên hình sau :

Mạch điều khiển khí nén được thiết kế như sau:
Xem thêm: Sửa Tivi Sony Huyện Thanh Trì

Hình 5. Mạch khí nén
Khi vẽ biểu đồ Karnaugh-Veitch cần quan tâm rằng :
- Phải chọn những vòng đối xứng, nếu cần có thể sử dụng cả những ô không xác định.
- Vòng càng lớn thì càng tốt vì phương trình thu được càng đơn giản.
Source: https://thomaygiat.com
Category : Điện Tử

Sửa Tivi Sony
Sửa Tivi Sony Dịch Vụ Uy Tín Tại Nhà Hà Nội 0941 559 995 Hà Nội có tới 30% tin dùng tivi sony thì việc…

Sửa Tivi Oled
Sửa Tivi Oled- Địa Chỉ Uy Tín Nhất Tại Hà Nội: 0941 559 995 Điện tử Bách Khoa cung cấp dịch vụ Sửa Tivi Oled với…

Sửa Tivi Samsung
Sửa Tivi Samsung- Khắc Phục Mọi Sự cố Tại Nhà 0941 559 995 Dịch vụ Sửa Tivi Samsung của điện tử Bách Khoa chuyên sửa…

Sửa Tivi Asanzo
Sửa Tivi Asanzo Hỗ Trợ Sử Lý Các Sự Cố Tại Nhà 0941 559 995 Dịch vụ Sửa Tivi Asanzo của điện tử Bách Khoa…

Sửa Tivi Skyworth
Sửa Tivi Skyworth Địa Chỉ Sửa Điện Tử Tại Nhà Uy Tín 0941 559 995 Điện tử Bách Khoa chuyên cung cấp các dịch vụ…

Sửa Tivi Toshiba
Sửa Tivi Toshiba Tại Nhà Hà Nội Hotline: 0948 559 995 Giữa muôn vàn trung tâm, các cơ sở cung cấp dịch vụ Sửa Tivi…
![Thợ Sửa Máy Giặt [ Tìm Thợ Sửa Máy Giặt Ở Đây ]](https://thomaygiat.com/wp-content/uploads/sua-may-giat-lg-tai-nha-1.jpg)
